ラプラス変換（Laplace transform）を使うと、微分方程式が代数的に解けてしまいます。「微分方程式が代数的に解ける」とは、解法が複雑だった微分方程式が
四則演算で解けるようになるということです。ラプラス変換を使って微分方程式を解いてく時の大まかな流れを下の図にまとめてみました。
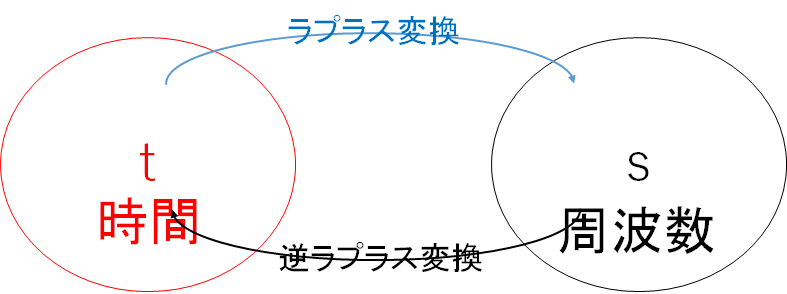
ある $t$ の関数 $f(t)$ （微分方程式で表される）を考えます。この $f(t)$ をラプラス変換すると、$s$ の関数 $F(s)$ （微分方程式ではない）となります。この $F(s)$ の式を計算して、整理したものを逆ラプラス変換すると、元の微分方程式 $f(t)$ が解けてしまいます。
ラプラス変換の定義は以下のようになります。
ある関数 $f(t)$ を考える。
ⅰ）$f(t)$ は $t \geqq $ において定義されており、区分的に連続である。
ⅱ）適当な整数 $a$ が存在して、$\displaystyle \int_{0}^{ \infty } |f(x)| e^{-at} dt \lt \infty$ を満たす。
ある関数 $f(t)$ が上記2つを満たすとき、$f(t)$ のラプラス変換は次のように定義される。
\[F(s) = \displaystyle \int_{0}^{\infty}e^{-st} f(t)dt\]
定義式から、ラプラス変換は、 $t≧0$ で定義された関数 $f(t)$ から、無限積分を使って新しい関数 $F(s)$ を作る操作であることがわかります。
関数 $f(t)$ をラプラス変換すると、 $F(s)$ になります。この関数 $F(s)$ のことを「関数 $f(t)$ のラプラス変換」と呼び、$L[f(t)]$ のように表記します。先頭にある $L$ はラプラス(Laplace)の頭文字です。
ここでは、ラプラス変換の定義式を使って、簡単な関数のラプラス変換にチャレンジしてみましょう。
本項の内容は、以下の動画でも詳しく解説しています。
問１ $f(t) = 1$ （定数） をラプラス変換せよ。
$f(t) = 1$ をラプラス変換の定義式に代入すると
$L[1] = \displaystyle \int_{0}^{\infty} e^{-st} 1 dt = \left[ -\dfrac{e^{-st}}{s} \right]_{t = 0}^{t = \infty} = -\displaystyle \lim_{t \to \infty} \dfrac{e^{-st}}{s} + \dfrac{1}{s} = \dfrac{1}{s}$
問２ $f(t) = e^{at}$ （指数関数）をラプラス変換せよ。
$f(t) = e^{at}$ をラプラス変換の定義式に代入すると
$F(s) = \displaystyle \int_{0}^{\infty} e^{-st} e^{at} dt = \displaystyle \int_{0}^{\infty} e^{-(s-a)t} dt = -\dfrac{1}{s-a} \left[ e^{-(s-a)t} \right] = -\dfrac{1}{s-a} (\displaystyle \lim_{t \to \infty} e^{-(s-a)t} - e^0)$
ここで、複素変数 $s$ の実部 $Re(s)$ が $Re(s) > a$ のとき、$\displaystyle \lim_{t \to \infty} e^{-(s-a)t}$ が $0$ となるので
$L[e^{at}] = \dfrac{1}{s-a}$
となります。
問３ $f(t) = \cos at$ （三角関数）をラプラス変換せよ。
今回は、ラプラス変換の定義式を使わずに計算してみましょう。$e^{iat}$ と $e^{-iat}$ はオイラーの公式を利用して、以下のようになります。
$e^{iat} = \cos at + i \sin at$
$e^{-iat} = \cos at - i \sin at$
これらの式から $\cos at$ を計算すると
$\cos at = \dfrac{e^{iat} + e^{-iat}}{2}$
となります。この式をラプラス変換すると、ラプラス変換の線形性から
$L[\cos at] = L[\dfrac{e^{iat} + e^{-iat}}{2}] = \dfrac{1}{2} L[e^{iat}] + \dfrac{1}{2} L[e^{-iat}]$
となります。上でやったように、指数関数のラプラス変換は $L[e^{at}] = \dfrac{1}{s-a}$ となるので、
$L[\cos at] = \dfrac{1}{2} \dfrac{1}{s-ia} + \dfrac{1}{2} \dfrac{1}{s+ia} = \dfrac{1}{2} \dfrac{s+ia + s-ia}{(s-ia)(s+ia)} = \dfrac{1}{2} \dfrac{2s}{s^2 + a^2} = \dfrac{2s}{s^2 + a^2}$
となります。
ラプラス変換について、さらに詳しく学びたい方には、以下の本がおすすめです（楽天のサイトにとびます）。
上で学んだように、ラプラス変換の定義式を使って、関数のラプラス変換を求められることはわかりました。しかし、毎回、関数を定義式に入れて計算するのはとても面倒です。そこで必要になるのがラプラス変換表です。
基本的な関数のラプラス変換は、すでに優秀な先人たちが証明してしてくれており、変換ルールがまとめられています。証明過程を理解することも大切なのですが、初学者にとっては、ラプラス変換表を使って微分方程式を解けるようになることが最優先だと個人的に思っています。最初のうちは「先人が証明したものを再証明する必要はない」と割り切ってラプラス変換表を覚え、何度も計算練習をするのが良いです。
ラプラス変換表を使って微分方程式を解けるようになることが最も重要です。
| $f(t)$ | $F(s)$ | $条件$ |
|---|
| $1$ | $\dfrac{1}{s}$ | $s>0$ |
| $t^n$ | $\dfrac{n!}{s^{n+1}}$ | $s>0, n=0,1,2,\cdots$ |
| $t^{\alpha}$ | $\dfrac{\Gamma(\alpha+1)}{s^{\alpha+1}}$ | $\alpha>-1, s>0$ |
| $e^{at}$ | $\dfrac{1}{s-a}$ | $s>a$ |
| $\sin at$ | $\dfrac{a}{{s^2}+{a^2}}$ | $s>0$ |
| $\cos at$ | $\dfrac{s}{{s^2}+{a^2}}$ | $s>0$ |
| $\sinh at$ | $\dfrac{a}{{s^2}-{a^2}}$ | $s>a,a≧0$ |
| $\cosh at$ | $\dfrac{s}{{s^2}-{a^2}}$ | $s>0,a≧0$ |
それでは、ラプラス変換表を使って簡単な計算練習をしてみましょう。
問４ $f(t) = 5e^{2t}$ をラプラス変換せよ。
$e$ がでてきたので、 $L[e^{at}] = \dfrac{1}{s-a} $ を使います。 すると、$a = 2$ となるので
$L[5e^{2t}] = \dfrac{5}{s-2}$
となります。ラプラス変換の定義式を使うより、はるかに簡単に答えが求まりました。
問５ $f(t) = 3t^{-\frac{1}{2}}$ をラプラス変換せよ。
$t$ の肩に乗っている指数が分数になっているので $L[t^\alpha] = \dfrac{\Gamma(\alpha+1)}{s^{\alpha+1}} $ を使います。 $\Gamma(\alpha)$ はガンマ関数といいます。ガンマ関数について詳しく知りたい方は
ガンマ関数 のページをご覧になってください。
$\Gamma(\frac{1}{2}) = \sqrt{\pi}$ として計算してください。
$L[3t^{-\frac{1}{2}}] = 3 L[t^{-\frac{1}{2}}] = 3 \dfrac{\Gamma(-\frac{1}{2})}{s^{-\frac{1}{2} + 1}} = 3 \dfrac{\Gamma(\frac{1}{2})}{s^{\frac{1}{2}}} = 3 \sqrt{\dfrac{\pi}{s}} $
ラプラス変換では、線形法則と相似法則が成り立ちます。
線形法則
$L[{af(t)+bg(t)}] = a F(s) + b G(s) (s>max(\alpha1,\alpha2))$
相似法則 $L[{af(t)}] = \dfrac{1}{a}F(\dfrac{s}{a}) (s>\alpha{a})$
以下に、ラプラス変換の第１移動法則と第２移動法則を示します。
第１移動法則 $L[{e^{\lambda{t}}f(t)}] = F(s-\lambda) (s>a+\lambda)$
第２移動法則 $L[U(t-\lambda)f(t-\lambda)]=e^{\lambda{s}}F(s) (s>a)$
以下に、ラプラス変換の微分法則を示します。
微分法則
$L[f^{(n)}(t)]=s^n L[f(t)]-s^{s-1}f(0)-\cdots-sf^{(n-2)}(0)-f^{(n-1)}(0) (s>\alpha)$
関数 $f(t)$ の $t$ に関する微分のラプラス変換は次のようになります。
$L \left[\dfrac{d}{dt}f(t) \right] = sF(s) - f(0)$
この式の $f(t)$ に $\dfrac{df(t)}{dt}$ を代入すると、次のようになります。
$L \left[\dfrac{d^2}{dt^2} f(t) \right] = L \left[ \dfrac{d}{dt} \{ \dfrac{d}{dt}f(t) \} \right] = sL \left[ \dfrac{df(t)}{dt} \right] - f^{(1)} (0)$
$= s^2 F(s) - sf(0) - f^{(0)}$
以下に、ラプラス変換の積分法則を示します。
積分法則
$L \left[\displaystyle \int_{0}^{t}f(u)du \right] = \dfrac{1}{s} L[f(t)] (s>max(0,\alpha))$
$t$ の領域で $f(t)$ を $t$ に関して積分するのは、$s$ の領域では $\dfrac{1}{s}$ をかけることに対応します。
以下に、ラプラス変換の$t$積法則を示します。
$t$積法則
$L[tf(t)]=-\dfrac{d}{ds}F(s) (s>\alpha)$
$t$ の領域で $f(t)$ に $t$ をかけるのは、$s$ の領域での微分に対応します。
$t^n$ 積法則
$L[t^{n}f(t)]=(-1)^{n}\dfrac{d^{n}}{ds^{n}}F(s) (s>\alpha)(n-1,2,3,\cdots)$
これらの性質を利用したラプラス変換の計算については以下の動画でも詳しく解説しています。
$f(t)$ , $g(t)$ は $t≧0$ で区分的に連続な関数とし、指数 $\alpha$ 位の関数とする。
